动态光散射中光子相关谱测量系统的空间相干性问题

关键词：光子相关谱；动态光散射；空间相干性；相干面积；信噪比

On the Spatial Coherence Problem of a photon Correlation Spectrum Measurement System in Dynamic Light Scattering
Wang Shaoqing Lou Benzhuo Tao Yewei Ren Zhongjing
(Science School of Jinan University Jinan 250022)
Abstract：Using a simplified model of light interference，we discussed the physical essence of the spatial coherence demand on a photon correlation spectrum measurement system in dynamic light scattering.By using the concept of “coherence area”，we standard-ized three familiar statement about the spatial coherence criterion on a photon correlation spectrum measurement system.In the end，we brought forward a general and compendious criterion.
Key words：photon correlation;dynamic light scattering;spatial coherence;coherence area;signal-noise ratio

动态光散射是研究大分子和亚微米颗粒在液体中动态行为的最有效方法。通过测量悬浮液中散射粒子产生的散射光中的微小频移和角度依赖性，可以获得表征高分子结构的丰富信息，也可以获得纳米微粒的平均流体力学半径和粒度分布。随着激光、微电子和计算机技术的发展，动态光散射技术得到了广泛的应用。由于散射光的频移很小(1-106Hz) ，用传统的光谱分析法难以分辨，所以在动态光散射实验中采用光子相关谱法来获得散射光的频移[1 - 5 ] 。
图1给出光子相关谱测量的基本实验装置。由激光器1发出的激光经聚焦后照射在样品池2中的散射粒子上，粒子的散射光经光学系统3后进入PMT(光电倍增管) 4 ，PMT 的光电脉冲经过甄别/ 放大系统5 进入相关器6 ，由相关器对光电脉冲进行相关处理后将相关数据输入计算机7 进行数据处理，得所需的信息。

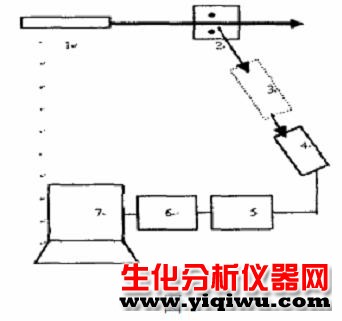
在光子相关谱测量中，PMT 输出信号1的信噪比(输出信号中涨落部分与噪声部分之比) 大小是测量成功与否的关键因素。而PMT 输出信号的信噪比大小又主要由测量系统的空间相干性来决定。对于光子相关谱测量系统空间相干性优劣的判别标准，不同的文献有各种不同的表述。其中比较有代表性的几种表述分别为：
（1）PMT的接受面积为一个相干面积[1，2，5，6]；
（2）从PMT处看散射区的截面为一个相干面积[7 ] ;
（3）PMT 接收到的散射光场的干涉图样限于一个极大到一个相邻的极小范围内[8] 。
这些表述方法的不同往往会造成一定程度的混乱。本文的主要目的就是在分析光子相关谱测量系统对空间相干性要求的物理本质基础上，研究这几种表述的相互关系，进而给出一个简明的统一表述。

光子相关谱测量系统空间相干性要求的物理本质

在动态光散射过程中，散射区内的每一个微粒使入射光发生散射，每一个微粒可视为一个二次光源。由于微粒的无规则热运动，使这些散射光的相位随机变化，故散射区可视为一个准单色非相干扩展光源。散射光场是所有微粒产生的散射光的叠加。随着散射微粒的无规则热运动，空间任意点的散射光场也将随机地涨落，正是这些涨落信号中，带有散射微粒的动力学信息。PMT 要探测的有用信号也就是这些涨落。如果PMT 探测到的信号中这些涨落不明显或被淹没，即信噪比很低，则测量是无意义的。那么，PMT 输出信号的信噪比由什么因素决定呢? 研究这个问题的途径有多种，本文从干涉的角度简明地加以讨论。
散射场可以视为由诸散射微粒发出的散射光的干涉场。某一时刻在空间某一点将有确定的干涉极大或极小。当然由于散射微粒的无规则热运动，这些极大和极小也是随机变化的，这就是散射场的随机涨落。如果PMT 的响应时间小于散射场随机涨落的时间， PMT 就能把这些涨落记录下来。如果PMT 接收面积较大，同时接收到多个干涉极大，则由于这些极大的随机变化，会使PMT 的输出信号趋于平坦，反映不出散射光场的涨落。当PMT 仅接收到一个干涉极大时，输出信号的涨落将最明显。所以，在设计光子相关谱测量系统时，要遵循这样一个
原则，即：限制PMT 的有效接收面积使其恰能接收到诸散射颗粒的散射光形成的一个干涉极大到相邻的干涉极小。当PMT 的有效接收面积大于或小于该面积时，信号的信噪比均将下降。这就是对光子相关谱测量系统空间相干性要求的物理本质。

光子相关谱测量系统的空间相干性判据

下面仍从光的干涉角度来研究这个问题。如图2所示，考虑散射区中相距最远的两个微粒，设其距离为d，PMT在散射角为φ的方向上接受散射光，PMT有效接收面积的线度为D，其到散射区中心的距离为L。
在L>>D和d及傍轴条件下，易于证明，两微粒的散射光在PMT接受面上中点O和边缘A处的光程差分别为：

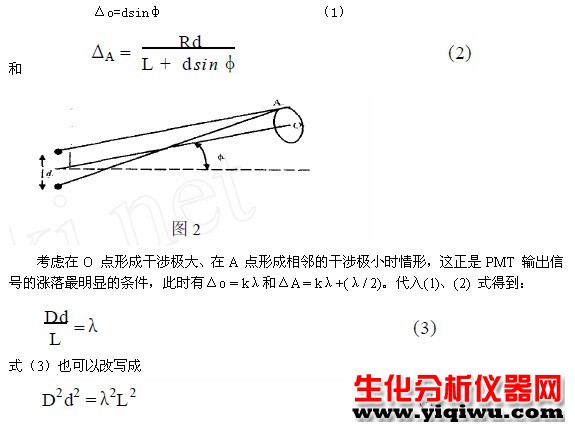
其中D2和d2可分别视为PMT的有效接受面积和散射区的等效截面积，分别用SPMT和Sd表示，则式（4）可写成
SPMTSd=λ2L2 （5）
式（5）的物理意义是：在设计光子相关谱测量系统时，为使PMT输出信号的信噪比最大，PMT的有效接收面积和从PMT处经光学系统看到的散射区的等效截面积之乘积应等于散射光平均波长与PMT到散射区距离乘积的平方。这就是光子相关谱测量系统的空间相干性判据。
应该指出，由于上面的讨论中采用了简化的干涉方法，加之散射区几何形状的多样性，式(5)是一个近似的结果。但无论采用何种研究方法，所得到的结论与式(5)基本相同，故式(5)可作为普遍的光子相关谱测量系统的空间相干性判据。

光子相干谱信号的信噪比与相干面积的关系

上面从干涉的角度研究了光子相关谱测量系统的空间相干性问题，认为在满足式（5）的条件下，光子相关谱测量系统的空间相干性最好，PMT输出信号的信噪比最佳。以下研究PMT输出信号的信噪比与光学中通常所说的相干面积的关系。
1.相干面积
相干面积是在研究准单色扩展光源的空间相干性问题时提出的概念。如图3所示


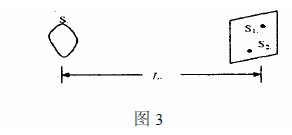
S代表中心波长为λ、面积为AS的准单色扩展光源，在距其为L的平面上的面积为AC的范围内任取两点S1和S2作为二次点光源。若由该两点光源产生的干涉场中干涉条纹的可见度不等于0 ，则称AC为光源S的相干面积。也就是说，面积AC内的任意两点的光场是相干的。由VanCittert Zernike定理可以证明[9] ，在L 远大于光源线度的条件下，相干面积AC可以近似表示为：


由式(6)可知，这个面积恰为将PMT 的有效面积视为扩展光源时的相干面积AC ，这就是光子相关谱测量系统空间相干性判据的表述2。至于表述3的含义前已讨论过。由此可见，本文所述的关于光子相关谱测量系统空间相干性判据的3 种表述，其物理含义是一样的。

利用相干立体角表述光子相关谱测量系统的空间相干性判据



其中SPMT/ L2 =Ω表示PMT的有效接收面积对散射区中心所张的立体角。则式(11)的物理意义为：当限制进入PMT的散射光恰在Ω=λ2/ Sd的立体角范围内时， PMT输出信号的信噪比最佳，或说光子相关谱测量系统的空间相干性最好。由相干立体角的定义式(9)可知，该立体角就是PMT的有效接收面积为一个相干面积时对应的相干立体角。
本文认为，由式(11) 表示光子相关谱测量系统的空间相干性判据是比较方便的。参见图1，在各种形式的光子相关谱测量系统中，为限定散射光的散射角和控制进入PMT的散射光，无论复杂或简单，光学系统3是必需的。此时，从PMT 直接接收到的是经光学系统3出射的散射光。这样，在考虑光子相关谱测量系统的空间相干性问题时，用式(11)比用式(5)来的清楚和方便。因为只需保证经光学系统3进入PMT的散射光被限制在一个相干立体角的范围内即可。但要注意此时式(11) 中的Sd应为光学系统3的出射光面积。



参考文献：

[1]J.Bruce,Dynamic Light Scattering(with applications to chemistry,biology,and physics) ,John Wiley & Sons, Inc. ,New York , 1976
[2]R.Pecora,Dynamic Light Scattering(Applications of Photon Correlation Spectroscopy) ,Plenum Press , New York , 1985
[3 ]周祖康,化学通报,1986 ,10 :34
[4 ]张渭滨,激光杂志,1991 ,12 (3) : 113
[5 ]左榘,激光散射原理及在高分子科学中的应用,河南科学技术出版社,1994
[6 ]左伟勋,中国科技大学硕士学位论文,1995 ,37
[7 ]周俊虎等,上海机械学院学报,1990 ,12 (3) :39
[8 ]李峰,浙江大学博士学位论文,1999 ,53
[9 ]金国藩等,激光测量学,科学出版社,1998 ,15